用牛顿迭代法求平方根

发表于   |   分类于   |     |   阅读次数

在LeetCode上面有一道Easy题，是sqrt(int x)，即求整数x的平方根。目前比较通用的一个方法就是采用牛顿迭代法来求平方根，它又被称为牛顿- 拉弗森方法，该方法主要思想就是 切线是曲线的线性逼近 。本文大致结构分为两部分，第一部分阐述牛顿迭代法的数学原理，第二部分简单说明如何在求平方根这一问题上应用牛顿迭代法，最后是一个简单总结。

牛顿迭代法

多数方程不存在求根公式，因此求精确根非常困难，甚至不可能，从而寻找方程的近似根就显得特别重要。

几何-代数推导

已知曲线，在点作切线，交轴于点，接着在点作切线交轴于点，图像如下：

牛顿迭代法

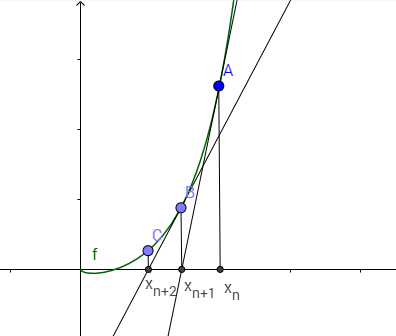
显然，点处的切线方程为，所以容易得到: ，求出点的值后，和上面一样的步骤，可以得到过点的切线方程，于是又可以得到点的值，这样不断迭代下去，直至无限逼近零点（即曲线与轴的交点）。

这种方法直觉上是对的，但是这里缺乏严格的数学证明，但这个其实已经被证明，来看看收敛的充分条件：

若二阶可导，那么在待求的零点周围存在一个区域，只要起始点位于这个邻近区间内，那么牛顿-拉弗森方法必定收敛。

和泰勒级数的关系

用牛顿迭代法解非线性方程，是把非线性方程线性化的一种近似方法。为什么这么说呢？这就要提起泰勒级数了(泰勒大法好啊，这辈子都会记住，毕竟在这儿栽过跟头)，我们把在点的某邻域内展开成泰勒级数：

取其线性部分，也就是泰勒展开的前两项，并令其等于0，即，以此作为非线性方程的近似方程，若一阶导数存在，且不为零（因为要做分母），则其解为，于是我们便得到了关于牛顿-拉弗森的一个迭代关系式：

可以发现，这个迭代公式和我们之前通过几何图推导出来的完全一致，这里要注意的是最后求出的零点并不是精确值，而是一个近似解，但是我们可以无限逼近精确值，这和极限的思想一个道理。

求平方根

前面简单的讲了牛顿迭代法的数学原理，如果有兴趣，可以点这里去仔细阅读关于牛顿迭代法更深层的本质，这里不再赘述。

有了这个利器，求平方根就非常简单了，高次方程的根其实也可以借此法求解（但是对函数特性有要求，二次函数可以收敛，这里不必担心）。假如我们要求，那怎么做呢？

步骤:

  • 令，则有方程;
  • 令，显然我们要求的就是曲线与轴的交点;
  • 随便给一个初值，根据这一迭代公式，可以计算出，…，那计算到什么时候停止呢？看下面：
  • 计算的增量的绝对值，即，根据题目要求的精度，我们可以设定当时便停止迭代，计算中止;
  • 此时得到的便为方程的根，即.

程序的实现

有了上述的基本分析后，就很容易写出代码了，采用c++编写如下，当然这里贴出的代码是对整数求平方根，不过对浮点数此法亦是可行的，只需更改一下精度即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int mySqrt(int x) {
        if(x<0){
            return 0x80000000; //x为负时，返回int的最小值
        }
        else if(x>1){
            double value_curr = x/2;
            double value_next = 0.0;
            double precise = 0.9;
            double diff = 1.0;
            while(diff > precise){
                value_next = (value_curr + x/value_curr)*0.5;
                diff = abs(value_curr - value_next);
                value_curr = value_next;
            }
            return int(value_next);
        }
        return x; // 0 or 1
    }
};

效率

在采用牛顿迭代法之前，我用一个类似于二分的思想撸了一个求平方根的方法（仅适用于正整数），运行效率还是相当的差，在这里也贴出比较愚的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {
public:
    int mySqrt(int x) {
        long right = x;
        long left = 0;
        long median = (right+left) / 2;
        map<int,bool> mp;
        if(x<0){
            return 0x80000000;
        }
        else if(x>1){
            while(1){
                if(median*median < x){
                    mp[median] = true;
                    left = median;
                    median = (right+left)/2;
                    if(mp[median]){
                        return median;
                    }
                }
                else if(median*median > x){
                    right = median;
                    median = (right+left)/2;
                    if(mp[median]){
                        return median;
                    }
                }
                else{
                    return median;
                }
            }
        }
        return x; // 0 or 1
    }
};

两种方法的运行效率相差很大，在同一测试集上跑，牛顿迭代法运行时间是3ms，二分思想(暂且就这么叫吧)是45ms，显然牛顿迭代法比二分思想的效率高达15倍，真是不知道比它高到哪里去了^_^。

贴一张关于两种方法的效率对比图
Efficiency comparison

总结

本文先简要阐述了牛顿迭代法的原理，再将其和泰勒级数的关系理了一下，最后着重说了一下如何利用牛顿迭代法求解平方根。当然，牛顿迭代法的用途主要是用来求解非线性方程的，而平方根只是其中一个特例，比如三次方、四次方程等等都可以用来求解。

坚持原创技术分享，您的支持将鼓励我继续创作！