leetcode-[Container With Most Water]

导读

这道算法题目非常有意思，秉着一题多解的思路和目标，我会分别给出算法时间复杂度分别为 $O(n^2)$ 和 $O(n)$ 的算法实现，并且在$O(n)$ 的基础上再优化，从而给出第三个解决方案，以节省程序运行时间。

问题描述

Given n non-negative integers $a_1$, $a_2$, …, $a_n$, where each represents a point at coordinate $(i, a_i)$. n vertical lines are drawn such that the two endpoints of line $i$ is at $(i, a_i)$ and $(i, 0)$. Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container.

问题解读

原问题的要求非常简单，假设我们把每条竖直线都当作是一个隔板，但是这些隔板的高度参差不齐，然后从中找出两条隔板，再加上对应的 $x$ 轴便可以形成一个容器，使得盛装的水量最大，即求的是找出两条竖线使得组成的容器容量达到最大。

Note:

盛水的容量取决于较短的那根隔板(竖线)和容器底部长度

这里的容量最大化可以等价转换为求面积最大化

时间复杂度为 $O(n^2)$ 的算法

这种解法最符合人类的第一直觉，也是最容易想到的办法，但是时间复杂度较高，不过作为一种解决方法，我们有必要去说清楚这种解法的思路。代码实现使用两层for循环便可搞定，思路如下。

思路:

假设左边的隔板是第 $i$ 个，右边的隔板是第 $j$ 个

$i$ 从最左边第一个开始向右，$j$ 从 $i+1$开始，直到遇到n结束，算出每一次的面积，并与当前的最大面积比较，如果新算出的面积比当前的最大面积要大，就更新最大面积为最新面积，并继续循环

面积公式: $s = min(a_i,a_j)*(j-i)$ , ( $0<i<j<n$ )

C++代码实现如下：

int maxArea(vector<int>& height) {
    int n = height.size();
    if(n <= 1){ //特殊情况
        return 0;
    }
    int area_max = 0;//最大面积
    int area_curr = 0;//当前面积
    for(int i=0; i<n-1; i++){
        int lheight = height[i];
        for(int j=i+1; j<n; j++){
            area_curr = min(lheight,height[j])*(j-i);
            if(area_curr > area_max){
                area_max = area_curr;
            }
        }
    }
    return area_max; //返回结果，即最大面积值
}

时间复杂度为 $O(n)$ 的算法

既然时间复杂度为 $O(n)$，也就是说我们只需要扫描一次数组(元素为每个隔板的高 $height$ )，即可得到最大面积，那就只能是通过两个指针来实现，一个指针left从左往右扫描，另一个指针right从右往左扫描，当两个指针在中间某个位置相遇时，跳出循环，结束并返回当前的面积。

这里隐含着一个问题，那就是在什么条件下移动左指针left和右指针right？其实道理很简单，那就是当哪个指针对应的隔板高度比另一个指针对应的隔板低时，我们就移动哪个指针。比如，左指针left对应的 $height[left] < height[right]$ ，下一步就移动left指针。可能有人会问了，那为何不移动对应隔板较高的指针呢？

Thinking:

无论移动的是左指针还是右指针，x轴对应的长度（容器底部长度）都必将减小。假设我们每次移动的是高隔板对应的指针，那么最大面积将只会出现在两个指针第一次处于左右端的初始时候，然而这里算出的最大面积并不一定是最大的，而且极有可能是错误的，因为下一个指针对应的隔板无论是比上一个指针对应的隔板大、相等、或是小，算出的面积都不会大于上一次算出的面积。造成这种情况的原因右两个：

x轴变短

容器的高度取决于较低的那个隔板的高

这里用的其实是一种简易的贪心策略，即我们每次保留高隔板对应的指针不动，而是移动矮隔板对应的指针，那么下一次出现的隔板才有可能使得面积变大，这就取决于下一次出现的隔板对应的高度了。

对应的代码如下：

int maxArea(vector<int>& height) {
    int n = height.size();
    if(n <= 1){
        return 0;
    }
    unsigned max_area = 0;
    size_t left=0, right = n-1;
    while(left < right){
        int area_curr = min(height[left],height[right])*(right-left);
        if(area_curr > max_area){
            max_area = water;
        }
        if(height[left] < height[right]){
            left++;
        }else{
            right--;
        }
    }
    return max_area;
}

运行时间截图如下：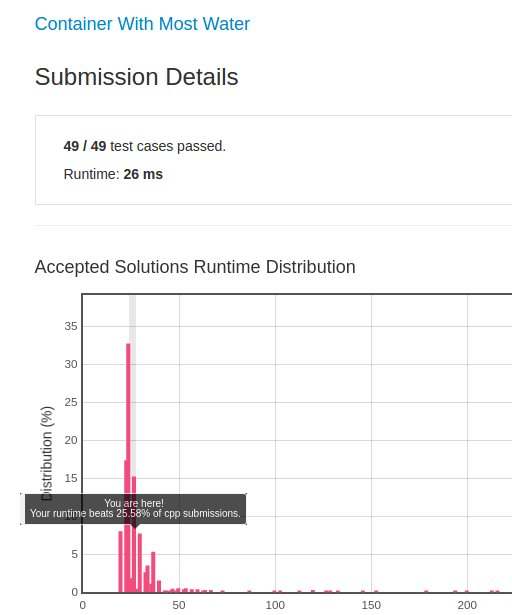

进一步优化时间复杂度为 $O(n)$ 的算法

在上面的算法基础之上，还可以稍微改动一下源码，便可以提高运行效率，节省时间。怎么做呢？

其实很简单，我们总是移动比较短的那根隔板对应的指针，为了尽快地找到比当前更大的面积，我们只需要保证下一次移动的指针所对应的隔板高度比之前的隔板高就行了，只有在这种情况下才有可能会比当前存储的面积要大，如果比之前的隔板还要低或者是等于之前的隔板，我们完全没有必要再去就算一遍此时新组成的容器对应的“面积”，每算一次乘法，就要耗费内存和CPU，这显然会降低速度。所以只需改一下判断条件就可以了，即如果当前的指针对应的隔板高度不大于之前的高度，就继续移动当前指针，直至找到一个比之前高的隔板才进行一次面积计算。核心代码如下：

while(left < right){
    int area_curr = min(height[left],height[right])*(right-left);
    if(area_curr > area_max){
        area_max = area_curr;
    }
    if(height[left] < height[right]){
        int left_value = height[left];
        left++;
        while(height[left] <= left_value && left<right){
            left++;
        }
    }else{
        int right_value = height[right];
        right--;
        while(height[right] <= right_value && left < right){
            right--;
        }
    }
}

运行时间截图如下：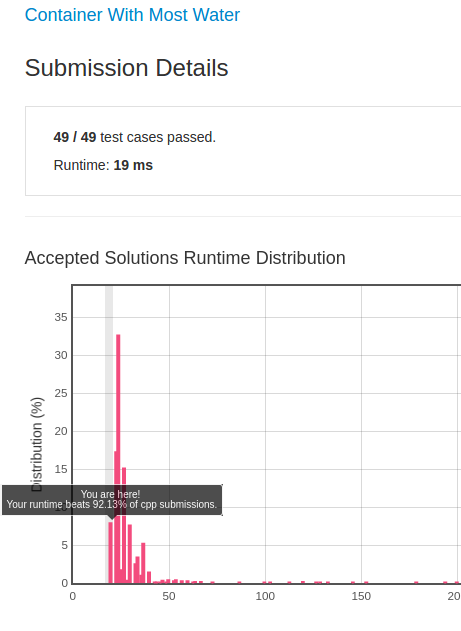

和上一张图对比，可以发现运行时间从26ms减小到19ms，在仅仅只有49个测试案例中，减少了7ms，运行效率提高了26.9%。显然，优化后的效果还是非常明显的。

总结

刷算法题目，不能仅仅局限于一种方法，如果发现自己的方法在submit后也AC了，而不注重运行效率，那就等于是白刷了算法题。当发现自己的算法运行时间非常低效时，这个时候就应该去想想是不是还有更厉害的解法，而这也恰恰是我们真正提高的机会。

这道题目之所以单独拿出来写，是因为此题比较高效的解法在直觉上不是那么让人可以容易且快速地理解，并且要严谨地论证一番这里的贪心策略可以达到全局最优，而非求得的是局部最优。

如果您对这道题目有更好的想法，欢迎发邮件给我，也可以在评论区聊哦！

戳这儿发现我的邮箱